jueves, 2 de diciembre de 2010
Exponentes fraccionarios
Vamos a demostarlo:
Si . Por definición de radical tenemos que .
Tomamoso raíces de orden n a cada lado de la igualdad:
Simplificamos ambos radicales dividiendo índice y exponente por n:
Ejemplos:
Escribe como exponente fraccionario:
Escribe en forma de radical
google_protectAndRun("render_ads.js::google_render_ad", google_handleError, google_render_ad);
jueves, 21 de octubre de 2010
que son los angulos rectos
Ángulo recto.
Un ángulo recto es aquel que mide 90° (sexagesimales). Su amplitud medida en otras unidades es: π/2 radianes y 100g (centesimales). Sus dos lados son dos semirrectas perpendiculares, y el vértice es el origen de dichas semirrectas.
Los ángulos rectos se encuentran en muchos elementos geométricos planos y objetos, por ejemplo:
Un triángulo rectángulo tiene un ángulo recto.
Un cuadrado tiene cuatro ángulos rectos.
Dos ángulos rectos forman un ángulo llano o plano, es decir, de 180°.
Cuatro ángulos rectos forman un ángulo completo o perigonal, es decir, de 360°.
Dos diámetros ortogonales de una circunferencia la dividen en cuatro cuadrantes; sus prolongaciones conforman cuatro ángulos rectos con vértice en el cento, cuyas amplitudes suman 360°.
miércoles, 20 de octubre de 2010
martes, 5 de octubre de 2010
ACOSO ESCOLAR
El acoso escolar puede ser físico.
El acoso escolar (también conocido como hostigamiento escolar, matonaje escolar o, incluso, por su término inglés bullying) es cualquier forma de maltrato psicológico, verbal o físico producido entre escolares de forma reiterada a lo largo de un tiempo determinado. Estadísticamente, el tipo de violencia dominante es el emocional y se da mayoritariamente en el aula y patio de los centros escolares. Los protagonistas de los casos de acoso escolar suelen ser niños y niñas en proceso de entrada en la adolescencia (12-13 años), siendo ligeramente mayor el porcentaje de niñas en el perfil de víctimas.
El acoso escolar es una forma característica y extrema de violencia escolar.
El acoso escolar es una especie de tortura, metódica y sistemática, en la que el agresor sume a la víctima, a menudo con el silencio, la indiferencia o la complicidad de otros compañeros.Este tipo de violencia escolar se caracteriza, por tanto, por una reiteración encaminada a conseguir la intimidación de la víctima, implicando un abuso de poder en tanto que es ejercida por un agresor más fuerte (ya sea esta fortaleza real o percibida subjetivamente) que aquella. El sujeto maltratado queda, así, expuesto física y emocionalmente ante el sujeto maltratador, generándose como consecuencia una serie de secuelas psicológicas (aunque estas no formen parte del diagnóstico); es común que el acosado viva aterrorizado con la idea de asistir a la escuela y que se muestre muy nervioso, triste y solitario en su vida cotidiana. En algunos casos, la dureza de la situación puede acarrear pensamientos sobre el suicidio e incluso su materialización, consecuencias propias del hostigamiento hacia las personas sin limitación de edad.
viernes, 1 de octubre de 2010
Figuras geométricas «sólidas» que delimitan volúmenes.
Figuras geométricas que delimitan superficies planas.
Una figura geométrica es un conjunto cuyos elementos son puntos.[1] La Geometría es el estudio matemático detallado de las figuras geométricas y sus características: forma, extensión, posición Las figuras geométricas más elementales
Las figuras geométricas más elementales son el punto, la recta y el plano. Mediante transformaciones y desplazamientos de sus componentes generan diversas líneas, superficies y volúmenes, que son objeto de estudio en matemáticas: geometría, topología, etc.
Adimensional (sin dimensiones)
Punto
Unidimensional (líneal)
Recta
semirrecta
segmento
Curva
Bidimensional (superficial)
Plano
Delimitan superficies (figuras geométricas en sentido estricto):
Polígono
triángulo
cuadrilátero
Sección cónica
elipse
circunferencia
parábola
hipérbola
Describen superficies:
Superficie de revolución
Superficie reglada
Tridimensional (volumétrico)
Delimitan volúmenes (cuerpos geométricos):
Poliedro
Describen volúmenes:
Sólido de revolución
cilindro
cono
esfera
N-dimensional (n dimensiones)
Politopo relativa, propiedades.
RAIZ CUADRADA
Representación de "raíz cuadrada de X".
En las ciencias matemáticas, se llama raíz cuadrada de un número (a veces abreviada como raíz a secas) a aquel otro que siendo mayor o igual que cero, elevado al cuadrado, es igual al primero.
La raíz cuadrada de x se expresa:
o bien:
Por ejemplo:
, ya que
, puesto que
Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que la raíz cuadrada de 2 era irracional (inconmensurable) o no expresable como cociente alguno, lo que supuso un hito en la matemática de la época.
Posteriormente se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de los números imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga todas sus raíces (teorema fundamental del álgebra). La diagonalización de matrices también permite el cálculo rápido de la raíz de una matriz.
Inicialmente mostraron su utilidad para la resolución de problemas trigonométricos y geométricos, como la diagonal de un cuadrado o el teorema de Pitágoras. Posteriormente fueron ganando utilidad para operar con polinomios y resolver ecuaciones de segundo grado o superior, siendo una de las herramientas matemáticas más elementales hoy en día.
jueves, 30 de septiembre de 2010
DE FINICIONES DE MATEMATICAS
Las diferentes definiciones suelen estar ligadas al área de trabajo, la más común y poco general es la definición de sucesión numérica, en la práctica se usan sucesiones de forma intuitiva:
[editar] Definición abstracta
Clase de finitos o numerables objetos ordenados.
[editar] Definición conjuntista
Una sucesión en un conjunto X es una enumeración de elementos de X, es decir una aplicación de en X.
[editar] Notación
Notaremos por a una sucesión, donde x la identifica como distinta de otra digamos .
La notación es permisiva en cuanto a su modificación si realmente es necesario.
[editar] Definición de término general
Llamaremos término general de una sucesión a ,donde indica el lugar que ocupa en dicha sucesión.
[editar] Definición de parcial
Llamaremos parcial de a una sucesión donde
[editar] Ejemplos en distintas áreas
Estos ejemplos pretenden ser una pequeña muestra de la infinidad, propiamente dicha, de usos que tienen dichas sucesiones en matemáticas.
El trabajo interno en el desarrollo de cada tema en cada área obliga a diversificar el modo de nominar y notar las sucesiones, haciéndose frecuente el uso de índices, subíndices y superíndices para salvar la sobrecarga de notación y hacerlas más legibles y estéticas en cuanto a la presentación.
[editar] En
Se puede tener una sucesión tal que
[editar] En el espacio de las sucesiones finitas en
Se puede tener una sucesión tal que
[editar] En K[x]
Un polinómio no es más que una sucesión finita tal que representada como .
[editar] En
Se puede tener una sucesión tal que , donde .
[editar] En un espacio vectorial topológico
Se puede tener una sucesión , donde , donde es una sucesión real arbitraria y B un abierto.
[editar] Sucesiones funcionales
Se puede tener una sucesión de funciones continuas .
[editar] En el lenguaje proposicional
Sea un alfabeto, llamaremos al conjunto de sucesiones finitas de n elementos de A, se define inductivamente por la sucesión de productos cartesianos siguiente:
así :={},a_n{>}\in A^n {,y\;} a_i:={}\in A" src="http://upload.wikimedia.org/math/9/5/7/9572c42f3b53269a0d3c9dc6d5518fae.png">.
[editar] En homología simplicial
El complejo de cadenas simplicial del complejo simplicial K, no es más que una determinada sucesión de grupos abelianos y morfismos
[editar] En el lenguaje de las categorías
Sea una categoría, podemos tener una sucesión , donde .
[editar] Sucesiones numéricas
Una sucesión numérica se formaliza como una aplicación de los naturales en los reales, es decir :
que escribiremos simplemente como o, si se da por entendido que los subíndices son enteros, también vale .
El nombre que recibe la sucesión también puede hacer referencia a los valores que toma sobre los reales, así, si la imagen de fuesen los racionales, es decir fracciones enteras del tipo , podemos llamarla sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, ... .
[editar] Notas y ejemplos básicos
Para definir término a término la sucesión, se indica para cada termino el valor que le corresponde directamente:
El primero es a por ejemplo 3,
el segundo es a por ejemplo -10,
el tercero es a por ejemplo 9, y así sucesivamente.
Para indicar, si hace falta, el comportamiento del resto de los valores, se usa el término general y se escribe acompañado como a por ejemplo número al azar, ... .
Los puntos suspensivos dan por entendido que los valores de la sucesión se omiten ya que estos quedan claramente determinados hasta el infinito, siendo el n-ésimo valor, , el portador del método para generar el valor de cada término, y el nombre puede ser cambiado, si hace falta, por , , , , ... .
Materialmente seria: 3, -10, 9, 7, ... , número al azar, ... .
[editar] Sucesión finita
Diremos que una sucesión es finita si determinamos su último termino, por ejemplo el n-ésimo:
Genéricamente: , donde sería el término general si hiciese falta.
ejemplo: 100, 99, 98, ... , 1, 0.
[editar] Sucesión constante
Diremos que una sucesión es constante si todos los términos valen , un número real cualquiera, ejemplo:
Genéricamente .
ejemplo: si queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.
[editar] Sucesión creciente
Si imponemos al termino general, de una sucesión numérica, la condición que , es decir, que el siguiente término, , siempre sea mayor estricto que su predecesor, , se llaman sucesiones estrictamente crecientes:
Para naturales: 1, 2, 3, 4, 5, 6, ... .
Para enteros: -10, -9, -8, -7, -6, ... .
Para reales: .
Si imponemos , es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
[editar] Sucesión decreciente
Al igual que las crecientes tenemos, según el termino general, que:
si entonces la sucesión es decreciente,
si a_{i+1}" src="http://upload.wikimedia.org/math/9/d/4/9d460ffb01e4c54999b7e5ef31245592.png"> es estrictamente decreciente.
[editar] Sucesión alternada
Intuitivamente se llama sucesión alternada cuando alterna valores de signo opuesto, como an = ( − 1)n que nos genera la sucesión: 1, -1, 1, -1, 1, -1, ... . Utilizado por las series llamadas series alternas.
[editar] Según el término general
El termino general de la sucesión queda definido de forma explícita si su valor está en función del valor del subíndice, es decir, si donde es una función cualquiera como por ejemplos:
que daría la sucesión de naturales sucesivos, es decir, 1, 2, 3, 4, 5, ... .
que daría todos los número pares incluido el cero, es decir, 0, 2, 4, 6, 8, ... .
que daría la sucesión de cuadrados siguiente, 0, 1, 4, 9, 16, ... .
Dada una función , llamaremos extensión en los reales de a una función cuyos valores coinciden en el dominio de , es decir, .
Error fatal es nombrar a la extensión en los reales con el mismo nombre ¡!, pues, se trata de una asociación totalmente arbitraria y no univoca que trae confusión y no tiene sentido para algunas funciones definidas a trozos. Compruébese que solo si la sucesión que determinan sobre los enteros es la misma, pero ¡no son la misma función!, llamemos a la extendida por ejemplo o si es un polinomio, o o si son funciones trigonométricas, agregando subíndices si hace falta.
La función f puede adquirir propiedades de la extendida P, si existe P con dichas propiedades, como límites al infinito, monotonía, acotaciones... .
Casos en los que f no puede extenderse sobre los reales:
si definimos un como el número de factores propios de n.
funciones aritméticas, como la función fi de Euler o la Función de Möbius µ.
El término general de la sucesión queda definido de forma implícita si su valor depende de sus predecesores, esto se indica en general del modo siguiente:
Dados previamente los valores de , podemos definir el término general de forma inductiva como = n" src="http://upload.wikimedia.org/math/0/f/9/0f92fd30b401f46dd4d7095756fabe43.png"> como por ejemplo con la ecuación en diferencias = n, \; a_0, \; ... \; , \; a_n, \; b_n \in \mathbb{R} " src="http://upload.wikimedia.org/math/e/d/1/ed10e8accf3c63d948fbfb391afbdf2a.png">.
QUE SON LAS FIGURAS GEOMETRICAS
Figuras geométricas «sólidas» que delimitan volúmenes.
Figuras geométricas que delimitan superficies planas.
Una figura geométrica es un conjunto cuyos elementos son puntos.[1] La Geometría es el estudio matemático detallado de las figuras geométricas y sus características: forma, extensión, posición relativa, propiedades.
Contenido[ocultar]
1 Historia y utilidad
2 Las figuras geométricas más elementales
3 Véase también
4 Notas
5 Enlaces externos
//
[editar] Historia y utilidad
La observación de la naturaleza nos muestra la existencia de variadas formas en los cuerpos materiales que la componen y nos proporciona la idea de volumen, superficie, línea, y punto. Por necesidades prácticas, el desarrollo de técnicas usadas para medir, construir o desplazarse, llevaron al hombre a hacer uso de las diversas propiedades de las figuras geométricas.
Una vez adquiridas estas nociones y prescindiendo de su origen práctico, la Geometría (medición de la tierra), de ser un conjunto de técnicas, pasó a constituir una disciplina matemática formal, donde la figura geométrica es un ente abstracto y sus propiedades el objeto de estudio de la Geometría.
Su aplicación práctica se estudia en física, mecánica, astronomía, náutica, topografía, balística, etc.
QUE ES EL ALGEBRA
Saltar a navegación, búsqueda
Para los usos matemáticos de la palabra álgebra como estructura algebraica, véase álgebra no asociativa, álgebra asociativa, álgebra sobre un cuerpo.
El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). Es una de las principales ramas de la matemática, junto a la geometría, el análisis matemático, la combinatoria y la teoría de números.
La palabra «álgebra» es de origen árabe, deriva del tratado escrito por el matemático persa Muhammad ibn Musa al-Jwarizmi, titulado Kitab al-yabr wa-l-muqabala (en árabe كتاب الجبر والمقابلة) (que significa "Compendio de cálculo por el método de completado y balanceado"), el cual proporcionaba operaciones simbólicas para la solución sistemática de ecuaciones lineales y cuadráticas. Etimológicamente, la palabra «álgebra» جبر (yabr) , proviene del árabe y significa "reducción".
martes, 28 de septiembre de 2010
La geometría es una de las más antiguas ciencias. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. En el Antiguo Egipto estaba muy desarrollada, según los textos de Heródoto, Estrabón y Diodoro Sículo. Euclides, en el siglo III a. C. configuró la geometría en forma axiomática, tratamiento que estableció una norma a seguir durante muchos siglos: la geometría euclidiana descrita en «Los Elementos».
El estudio de la astronomía y la cartografía, tratando de determinar las posiciones de estrellas y planetas en la esfera celeste, sirvió como importante fuente de resolución de problemas geométricos durante más de un milenio. René Descartes desarrolló simultáneamente el álgebra y la geometría, marcando una nueva etapa, donde las figuras geométricas, tales como las curvas planas, podrían ser representadas analíticamente, es decir, con funciones y ecuaciones. La geometría se enriquece con el estudio de la estructura intrínseca de los entes geométricos que analizan Euler y Gauss, que condujo a la creación de la topología y la geometría diferencial.
QUE SON LAS MATEMATICAS
Euclides, matemático griego, del siglo III a. C., tal como fue imaginado por Rafael. Detalle de La Escuela de Atenas.[1]
Las matemáticas o la matemática (del lat. mathematĭca, y éste del gr. μαθηματικά, derivado de μάθημα, conocimiento) es una ciencia que, partiendo de axiomas y siguiendo el razonamiento lógico, estudia las propiedades y relaciones cuantitativas entre los entes abstractos (números, figuras geométricas, símbolos).[2] Mediante las matemáticas conocemos las cantidades, las estructuras, el espacio y los cambios. Los matemáticos buscan patrones,[3] [4] formulan nuevas conjeturas e intentan alcanzar la verdad matemática mediante rigurosas deducciones. Éstas les permiten establecer los axiomas y las definiciones apropiados para dicho fin.[5]
Existe cierto debate acerca de si los objetos matemáticos, como los números y puntos, realmente existen o si provienen de la imaginación humana. El matemático Benjamin Peirce definió las matemáticas como "la ciencia que señala las conclusiones necesarias".[6] Por otro lado, Albert Einstein declaró que "cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad".[7]
martes, 8 de junio de 2010
Que es la area
Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial.
Para poder definir el área de una superficie en general –que es un concepto métrico–, se tiene que haber definido un tensor métrico sobre la superficie en cuestión: cuando la superficie está dentro de un espacio euclídeo, la superficie hereda una estructura métrica natural inducida por la métrica euclídea.
jueves, 25 de marzo de 2010
CUERPOS GEOMETRICOS
CUADRILÁTEROS
Son figuras planas cerradas limitadas por cuatro lados, cuatro vértices y cuatro ángulos.
CUADRADO
Es la figura plana cerrada, limitada por cuatro lados iguales y cuatro ángulos rectos.
RECTÁNGULO
Es la figura plana cerrada, limitada por cuatro lados iguales de dos en dos y cuatro ángulos rectos.
ROMBO
Es la figura plana cerrada, limitada por cuatro lados iguales, dos ángulos agudos y dos obtusos.
TRAPECIO
Es una figura plana cerrada limitada por cuatro lados, 2 paralelos y 2 no paralelos.
PARALELOGRAMO
Los paralelogramos tienen como característica general, que los lados opuestos son iguales y paralelos
PERÍMETRO
El perímetro de una figura es igual a la suma de sus lados.
Observa en la figura siguiente, si tenemos una figura de cuatro lados cuyos valores son 2 cm, 3 cm, 2 cm, 5 cm, el perímetro de la misma es 12 cm.
CUERPO GEOMÉTRICO
Es todo objeto que ocupa un lugar en el espacio y se halla limitado por superficies planas o curvas.
Son ejemplos de cuerpos geométricos: el cubo, la pirámide, el prisma, el cilindro, la esfera, el cono entre otros.
Observa en la figura siguiente estos cuerpos geométricos.
«123
HISTORIA DE LAS MATEMATICAS
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
Euclides, matemático griego, del siglo III a. C., tal como fue imaginado por Rafael. Detalle de La Escuela de Atenas.[1]
Las matemáticas o la matemática (del lat. mathematĭca, y éste del gr. μαθηματικά, derivado de μάθημα, conocimiento) es una ciencia que, a partir de notaciones básicas exactas y a través del razonamiento lógico, estudia las propiedades y relaciones cuantitativas entre los entes abstractos (números, figuras geométricas, símbolos).[2] Mediante las matemáticas conocemos las cantidades, las estructuras, el espacio y los cambios. Los matemáticos buscan patrones,[3] [4] formulan nuevas conjeturas e intentan alcanzar la verdad matemática mediante rigurosas deducciones. Éstas les permiten establecer los axiomas y las definiciones apropiados para dicho fin.[5]
Existe cierto debate acerca de si los objetos matemáticos, como los números y puntos, realmente existen o si provienen de la imaginación humana. El matemático Benjamin Peirce definió las matemáticas como "la ciencia que señala las conclusiones necesarias".[6] Por otro lado, Albert Einstein declaró que "cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad".[7]
Mediante la abstracción y el uso de la lógica en el razonamiento, las matemáticas han evolucionado basándose en las cuentas, el cálculo y las mediciones, junto con el estudio sistemático de la forma y el movimiento de los objetos físicos. Las matemáticas, desde sus comienzos, han tenido un fin práctico (véase: Historia de la matemática). Las explicaciones que se apoyaban en la lógica aparecieron por primera vez con la matemática helénica, especialmente con los Elementos de Euclides. Las matemáticas siguieron desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.
Hoy en día, las Matemáticas se usan en todo el mundo como una herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales, la ingeniería, la medicina y las ciencias sociales, e incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música (por ejemplo, en cuestiones de resonancia armónica). Las matemáticas aplicadas, rama de las matemáticas destinada a la aplicación de los conocimientos matemáticos a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas. Los matemáticos también participan en las matemáticas puras, sin tener en cuenta la aplicación de esta ciencia, aunque las aplicaciones prácticas de las matemáticas puras suelen ser descubiertas con el paso del tiempo.[8]
Contenido[ocultar]
1 Etimología
2 Historia
2.1 Grandes matemáticos de la historia
2.2 Influencia en la astronomía moderna
2.3 Crisis históricas
3 La inspiración, las matemáticas puras y aplicadas y la estética
4 Notación, lenguaje y rigor
5 La matemática como ciencia
6 Ramas de estudio de las matemáticas
7 Conceptos erróneos
8 Véase también
9 Referencias
10 Bibliografía
11 Enlaces externos
//
Etimología [editar]
La palabra "matemática" (del griego μαθηματικά, «lo que se aprende») viene del griego antiguo μάθημα (máthēma), que quiere decir «campo de estudio o instrucción». El significado se contrapone a μουσική (musiké) «lo que se puede entender sin haber sido instruido», que refiere a poesía, retórica y campos similares, mientras que μαθηματική se refiere a las áreas del conocimiento que sólo pueden entenderse tras haber sido instruido en las mismas (astronomía, aritmética).[9] Aunque el término ya era usado por los pitagóricos en el siglo VI a. C., alcanzó su significado más técnico y reducido de "estudio matemático" en los tiempos de Aristóteles (siglo IV a. C.). Su adjetivo es μαθηματικός (mathēmatikós), "relacionado con el aprendizaje", lo cual, de manera similar, vino a significar "matemático". En particular, μαθηματική τέχνη (mathēmatikḗ tékhnē; en latín ars mathematica), significa "el arte matemática".
La forma plural matemáticas viene de la forma latina mathematica (Cicerón), basada en el plural en griego τα μαθηματικά (ta mathēmatiká), usada por Aristóteles y que significa, a grandes rasgos, "todas las cosas matemáticas".
Historia [editar]
Artículo principal: Historia de la matemática
Instrumentos paracálculos matemáticos
AntiguosÁbacoÁbaco de NapierRegla de cálculoRegla y compásCálculo mental
NuevosCalculadorasOrdenadores:(Lenguajes de programaciónsoftware especializado)
La evolución de la matemática puede ser considerada como el resultado de un incremento de la capacidad de abstracción del hombre o como una expansión de la materia estudiada. Los primeros conceptos abstractos utilizados por el hombre, aunque también por muchos animales,[10] fueron probablemente los números. Esta noción nació de la necesidad de contar los objetos que nos rodeaban.
Desde el comienzo de la historia, las principales disciplinas matemáticas surgieron de la necesidad del hombre de hacer cálculos con el fin de controlar los impuestos y el comercio, comprender las relaciones entre los números, la medición de terrenos y la predicción de los eventos astronómicos. Estas necesidades están estrechamente relacionadas con las principales propiedades que estudian las matemáticas — la cantidad, la estructura, el espacio y el cambio. Desde entonces, las matemáticas han tenido un profuso desarrollo y se ha producido una fructífera interacción entre las matemáticas y la ciencia, en beneficio de ambas. Diversos descubrimientos matemáticos se han sucedido a lo largo de la historia y se continúan produciendo en la actualidad.
Además de saber contar los objetos físicos, los hombres prehistóricos también sabían cómo contar cantidades abstractas como el tiempo (días, estaciones, años, etc.) Asimismo empezaron a dominar la aritmética elemental (suma, resta, multiplicación y división).
Un quipu, utilizado por los Incas para registrar los números.
Los siguientes avances requirieron la escritura o algún otro sistema para registrar los números, tales como los tallies o las cuerdas anudadas —denominadas quipu —, que eran utilizadas por los Incas para almacenar datos numéricos. Los sistemas de numeración han sido muchos y diversos. Los primeros escritos conocidos que contienen números fueron creados por los egipcios en el Imperio Medio, entre ellos se encuentra el Papiro de Ahmes. La Cultura del valle del Indo desarrolló el moderno sistema decimal, junto con el concepto de cero.
Los antiguos babilonios utilizaban el sistema sexagesimal, escala matemática que tiene por base el número sesenta. De este sistema la humanidad heredó la división actual del tiempo: el día en veinticuatro horas - o en dos períodos de doce horas cada uno -, la hora en sesenta minutos y el minuto en sesenta segundos. Los árabes proporcionaron a la cultura europea su sistema de numeración, que reemplazó a la numeración romana. Este sistema prácticamente no se conocía en Europa antes de que el matemático Leonardo Fibonacci lo introdujera en 1202 en su obra Liber abbaci (Libro del ábaco). En un principio los europeos tardaron en reaccionar, pero hacia finales de la Edad Media habían aceptado el nuevo sistema numérico, cuya sencillez estimuló y alentó el progreso de la ciencia.
Los números mayas del 0 al 19.
Los mayas desarrollaron una avanzada civilización precolombina, con avances notables en la matemática, empleando el concepto del cero, y en la astronomía, calculando con bastante precisión los ciclos celestes.
Grandes matemáticos de la historia [editar]
Algunos de los matemáticos más emblemáticos han sido:
Tales de Mileto: (hacia el 600 a. C.). Matemático y geómetra griego. Considerado uno de los Siete Sabios de Grecia.
Inventor del Teorema de Tales, que establece que, si a un triángulo cualquiera le trazamos una paralela a cualquiera de sus lados, obtenemos dos triángulos semejantes. Dos triángulos son semejantes si tienen los ángulos iguales y sus lados son proporcionales, es decir, que la igualdad de los cocientes equivale al paralelismo. Este teorema establece así una relación entre el álgebra y la geometría.
Pitágoras: (582-500 a. C.). Fundador de la escuela pitagórica, cuyos principios se regían por el amor a la sabiduría, a las matemáticas y música.
Inventor del Teorema de Pitágoras, que establece que, en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los dos catetos (los dos lados del triángulo menores que la hipotenusa y que conforman el ángulo recto). Además del teorema anteriormente mencionado, también invento una tabla de multiplicar.
Euclides: (aproximadamente 365-300 a. C.). Sabio griego, cuya obra "Elementos de Geometría" está considerada como el texto matemático más importante de la historia.
Los teoremas de Euclides son los que generalmente se aprenden en la escuela moderna. Por citar algunos de los más conocidos:
- La suma de los ángulos interiores de cualquier triángulo es 180°.
- En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, que es el famoso teorema de Pitágoras.
LINEAS ABIERTAS Y CERRADAS
LINEAS ABIERTAS Y CERRADAS
Estas líneas sirven para formar figuras, cuando las líneas se combinan, y se unen el principio y el fin, se llaman líneas cerradas. Si se puede diferenciar en dos partes distintas, el principio y el fin de la línea, entonces son líneas abiertas.
Líneas cerradas
Líneas abiertas
Responde la siguiente pregunta: ¿Si cierras las líneas abiertas del dibujo anterior, qué obtienes? Mira dos ejemplos de objetos de la naturaleza, que puedas dibujar con líneas abiertas o líneas cerradas, por ejemplo, la luna, puedes dibujarla con una línea cerrada: Y las patas de un pollo, puedes dibujarlo usando líneas abiertas:
INTERIOR, EXTERIOR Y FRONTERA
Cuando tú tienes una línea cerrada, puedes observar otras cosas, que pueden estar dentro de esta línea cerrada, o en el interior, o fuera de la línea, o en el exterior. La línea cerrada, se llama frontera.
CONJUNTOS
Los objetos que se encuentran dentro de una línea cerrada y que cumplen con características comunes entre sí, como colores, formas, texturas o cualquier otra característica que tú conozcas, pueden formar un conjunto.
Los niños formaron tres grupos, y los pusieron en tres platos distintos, formando así, tres conjuntos, uno de galletas, otro de caramelos, y otro de bastones
MEDIDAS DE LONGITUD
Cuando medimos la longitud de un objeto, estamos viendo cuantas veces entra una unidad de medida en el largo del objeto. Para que todos obtengamos el mismo resultado debemos usar la misma unidad de medida. Para ello se creó una unidad principal de longitud llamada metro que es fija, universal e invariable. El sistema de unidades de medida que incluye al metro junto a sus múltiplos y submúltiplos se llama Sistema Métrico Decimal.
Para trabajar en álgebra son necesarios ciertos conocimientos previos sobre operatoria en Números Enteros y Números Racionales. También deben conocerse las propiedades de las potencias.
Los ejercicios deben desarrollarse de acuerdo a las operatorias que se realicen. Se pueden restar o sumar términos semejantes, multiplicar expresiones algebraicas o bien simplificarlas.
Símbolos y términos específicos
Entre los símbolos algebraicos se encuentran números, letras y signos que representan las diversas operaciones aritméticas.
Los números son, por supuesto, constantes, pero las letras pueden representar tanto constantes como variables. Las primeras letras del alfabeto se usan para representar constantes y las últimas para variables.
Operaciones y agrupación de símbolos
La agrupación de los símbolos algebraicos y la secuencia de las operaciones aritméticas se basa en los símbolos de agrupación, que garantizan la claridad de lectura del lenguaje algebraico.
Entre los símbolos de agrupación se encuentran los paréntesis (), corchetes [], llaves {} y rayas horizontales —también llamadas vínculos— que suelen usarse para representar la división y las raíces, como en el siguiente ejemplo:
Los símbolos de las operaciones básicas son bien conocidos de la aritmética: adición (+), sustracción (-), multiplicación (×) y división (:).
En el caso de la multiplicación, el signo ‘×’ normalmente se omite o se sustituye por un punto, como en a·b. Un grupo de símbolos contiguos, como abc, representa el producto de a, b y c.
La división se indica normalmente mediante rayas horizontales. Una raya oblicua, o virgulilla, también se usa para separar el numerador, a la izquierda de la raya, del denominador, a la derecha, en las fracciones.
Hay que tener cuidado de agrupar los términos apropiadamente.
Por ejemplo, ax + b/c - dy indica que ax y dy son términos separados, lo mismo que b/c, mientras que (ax + b)/(c - dy) representa la fracción.
lunes, 15 de febrero de 2010
raiz cuadrada
Definición de raíz cuadrada
La raíz cuadrada es la operación inversa a elevar al cuadrado y consiste en averiguar el número cuando se conoce su cuadrado.
![]()
Calculo de una raíz cuadrada
Calcular la raíz cuadrada de:
![]()
1Si el radicando tiene más de dos cifras, separamos las cifras en grupos de dos empezando por la derecha.
![]()
2 Calculamos la raíz cuadrada entera o exacta, del primer grupo de cifras por la izquierda.
¿Qué número elevado al cuadrado da 8?
8 no es un cuadrado perfecto pero está comprendido entre dos cuadrados perfectos: 4 y 9, entonces tomaremos la raíz del cuadrada del cuadrado perfecto por defecto: 2, y lo colocamos en la casilla correspondiente.
![]()
3El cuadrado de la raíz obtenida se resta al primer grupo de cifras que aparecen en el radicando.
 El cuadrado de 2 es 4. se lo restamos a 8 y obtenemos 4.
El cuadrado de 2 es 4. se lo restamos a 8 y obtenemos 4.
4 Detrás del resto colocamos el siguiente grupo de cifras del radicando, separando del número formado la primera cifra a la derecha y dividiendo lo que resta por el duplo de la raíz anterior.

Bajamos 92, siendo la cantidad operable del radicando: 492.
49 : 4 > 9, tomamos como resultado 9.
5 El cociente que se obtenga se coloca detrás del duplo de la raíz, multiplicando el número formado por él, y restándolo a la cantidad operable del radicando.

Si hubiésemos obtenido un valor superior a la a la cantidad operable del radicando, habríamos probado por 8, por 7... hasta encontrar un valor inferior.

6 El cociente obtenido es la segunda cifra de la raíz.

7 Bajamos el siguiente par de cifras y repetimos los pasos anteriores.

Como 5301 > 5125, probamos por 8.

Subimos el 8 a la raíz

8Prueba.
Para que el resultado sea correcto, se tiene que cumplir:
Radicando= (Raíz entera)2 + Resto
89 225 = 2982 + 421
Ejercicios de raíces cuadradas
Resolver la raíz cuadrada de:


Calcular la raíz cuadrada de:


Resolver la raíz cuadrada de:


numeros naturales
Número natural
De Wikipedia, la enciclopedia libre
Un número natural es cualquiera de los números que se usan para contar los elementos de un conjunto (el cero es el número de elementos del conjunto vacío). Reciben ese nombre porque fueron los primeros que utilizó el ser humano para contar objetos.
Algunos matemáticos (especialmente los de Teoría de Números) prefieren no reconocer el cero (0) como un número natural; otros, especialmente los de Teoría de conjuntos, Lógica e Informática, sostienen la postura opuesta.
Contenido[ocultar] |
Definiciones [editar]
- La Real Academia Española los define como "Cada uno de los elementos de la sucesión 0, 1, 2, 3..." [1]
- Es el conjunto de los números enteros no negativos.
- Un número es un símbolo que indica una cantidad
. El conjunto de los números naturales se representa por 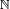 y corresponde al siguiente conjunto numérico:
y corresponde al siguiente conjunto numérico:
Los números naturales son un conjunto cerrado para las operaciones de la adición y la multiplicación, ya que al operar con cualquiera de sus elementos, resulta siempre un número perteneciente a 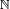 .
.
Historia [editar]
Antes de que surgieran los números para la representación de cantidades, el ser humano usó otros métodos para contar, utilizando para ello objetos como piedras, palitos de madera, nudos de cuerdas, o simplemente los dedos. Más adelante comenzaron a aparecer los símbolos gráficos como señales para contar, por ejemplo marcas en una vara o simplemente trazos específicos sobre la arena. Pero fue en Mesopotamia alrededor del año 4.000 a. C. donde aparecen los primeros vestigios de los números que consistieron en grabados de señales en formas de cuñas sobre pequeños tableros de arcilla empleando para ello un palito aguzado. De aquí el nombre de escritura cuneiforme. Este sistema de numeración fue adoptado más tarde, aunque con símbolos gráficos diferentes, en la Grecia Antigua y en la Antigua Roma. En la Grecia antigua se empleaban simplemente las letras de su alfabeto, mientras que en la antigua Roma además de las letras, se utilizaron algunos símbolos.
Quien colocó al conjunto de los números naturales sobre lo que comenzaba a ser una base sólida, fue Richard Dedekind en el siglo XIX. Este los derivó de una serie de postulados (lo que implicaba que la existencia del conjunto de números naturales se daba por cierta), que después precisó Peano dentro de una lógica de segundo orden, resultando así los famosos cinco postulados que llevan su nombre. Frege fue superior a ambos, demostrando la existencia del sistema de números naturales partiendo de principios más fuertes. Lamentablemente la teoría de Frege perdió, por así decirlo, su credibilidad y hubo que buscar un nuevo método. Fue Zermelo quien demostró la existencia del conjunto de números naturales, dentro de su teoría de conjuntos y principalmente mediante el uso del axioma de infinitud que, con una modificación de este hecha por Adolf Fraenkel, permite construir el conjunto de números naturales como ordinales según von Neumann.
GEOMETRIA
GEOMETRIA
Altura de los triángulos.
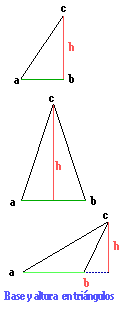 |
En geometría es usual designar la altura de una figura empleando la letra H, probablemente con referencia a la palabra francesa hauteur (se pronuncia: otér), que precisamente significa altura. |
Altura de los cuadriláteros.
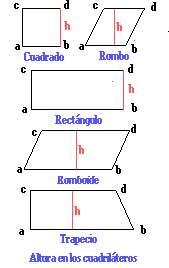 |
|
Igualdad y semejanza en las figuras geométricas.
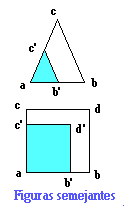 |
|
Diagonal y mediana de los cuadriláteros.
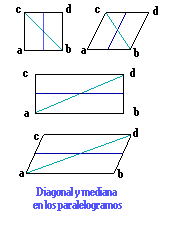 |
|


